Question

Suppose after 2500 years an initial amount of 1000 grams of a radioactive substance has decayed to 75 grams. What is the half-life of the substance? The half-life is:_______.

(A) Less than 600 years
(B) Between 600 and 700 years
(C) Between 700 and 800 years
(D) Between 800 and 900 years
(E) More than 900 years

Answer 1

The correct answer is:

Between 600 and 700 years (B)

Explanation:

At a constant decay rate, the half-life of a radioactive substance is the time taken for the substance to decay to half of its original mass. The formula for radioactive exponential decay is given by:

`A(t) = A_0 e^((kt))\\where:\\A(t) = Amount\ left\ at\ time\ (t) = 75\ grams\\A_0 = initial\ amount = 1000\ grams\\k = decay\ constant\\t = time\ of\ decay = 2500\ years`

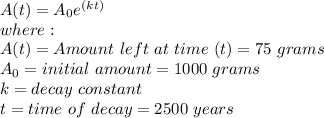
First, let us calculate the decay constant (k)

`75 = 1000 e^((k2500))\\dividing\ both\ sides\ by\ 1000\\0.075 = e^((2500k))\\taking\ natural\ logarithm\ of\ both\ sides\\In 0.075 = In (e^(2500k))\\In 0.075 = 2500k\\k = (In0.075)/(2500)\\ k = (-2.5903)/(2500) \\k = - 0.001036`

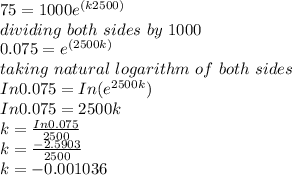
Next, let us calculate the half-life as follows:

`(1)/(2) A_0 = A_0 e^((-0.001036t))\\Dividing\ both\ sides\ by\ A_0\\ (1)/(2) = e^(-0.001036t)\\taking\ natural\ logarithm\ of\ both\ sides\\In(0.5) = In (e^(-0.001036t))\\-0.6931 = -0.001036t\\t = (-0.6931)/(-0.001036) \\t = 669.02 years\\\therefore t(1)/(2) \approx 669\ years`

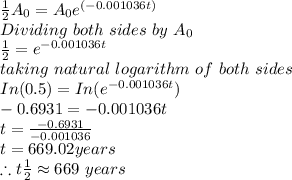
Therefore the half-life is between 600 and 700 years