Question

Low‑density lipoprotein, or LDL, is the main source of cholesterol buildup and blockage in the arteries. This is why LDL is known as "bad cholesterol." LDL is measured in milligrams per deciliter of blood, or mg/dL. In a population of adults at risk for cardiovascular problems, the distribution of LDL levels is normal, with a mean of 123 mg/dL and a standard deviation of 41 mg/dL. If an individual's LDL is at least 1 standard deviation or more above the mean, he or she will be monitored carefully by a doctor. What percentage of individuals from this population will have LDL levels 1 or more standard deviations above the mean?

Answer 1

The percentage of individuals from this population will have LDL levels 1 or more standard deviations above the mean is 16%.

Explanation:

Let X represent the LDL levels.

It is provided that
`X\sim N(123, 41^(2))`.

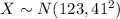Compute the probability that a randomly selected individual is will have LDL levels 1 or more standard deviations above the mean as follows:

`P(X\geq \mu+\sigma)=P(X\geq 123+41)`

`=P(X\geq 164)\\\\=P((X-\mu)/(\sigma)\geq (164-123)/(41))\\\\=P(Z>1)\\\\=1-P(Z<1)\\\\=1-0.84134\\\\=0.15866\\\\\approx 0.16`

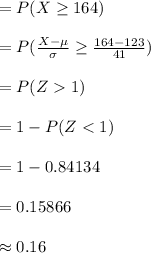
Thus, the percentage of individuals from this population will have LDL levels 1 or more standard deviations above the mean is 16%.