Question

A length of 20-gauge copper wire (of diameter 0.8118 mm) is formed into a circular loop with a radius of 25.0 cm. A magnetic field perpendicular to the plane of the loop increases from zero to 10.0 mT in 0.34 s. Find the average electrical power dissipated in the process

Answer 1

The average electrical power dissipated in the process is 0.653 mW

Step-by-step explanation:

Given;

gauge of copper wire, 20 gauge

resistivity from chart,
`\rho = 1.68 *10^(-8) \ ohm.m`

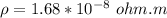
radius of the circular loop, r = 25 cm

magnetic field strength, B = 10 .0 mT

time, t = 0.34 s

Length of the wire, L = 2πr = 2 x π x 0.25 = 1.571 m

Area of the wire, A = πR² ⇒ R = D/2 = 0.8118 mm/ 2 = 0.4059 mm

= π(0.4059 x 10⁻³)² = 0.5177 x 10⁻⁶ m²

The resistance of the wire is given by;

`R = (\rho L)/(A)\\\\ R = (1.68*10^(-8)*1.571)/((0.5177*10^(-6)))\\\\ R = 5.098 *10^(-2) \ ohms`

Now, determine the electric potential;

`E = N(d\phi)/(dt)\\\\ E = N((BA)/(dt))\\\\ E = 1(((10*10^(-3))(\pi*0.25^2))/(0.34) )\\\\E = 0.00577 \ V`

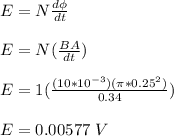
The average power is given by;

P = V²/R

P = (0.00577²) / (5.098 x 10⁻²)

P = 6.53 x 10⁻⁴ W

P = 0.653 mW

Therefore, the average electrical power dissipated in the process is 0.653 mW