Answer:
 is equivalent to
is equivalent to
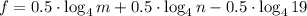 .
.
Explanation:
Let be
 , we transform this into an equivalent expression with sums and differences of logarithms by applying logarithm properties:
, we transform this into an equivalent expression with sums and differences of logarithms by applying logarithm properties:
1)
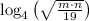 Given.
Given.
2)
![\log_(4)\left[\left((m\cdot n)/(19) \right)^(0.5)\right]](https://img.qammunity.org/2021/formulas/mathematics/college/v26oo9h93rer6ohhexss6d7x7d1qctanh7.png) Definition of square root.
Definition of square root.
3)
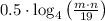

4)
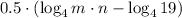
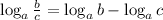
5)
 Distributive property.
Distributive property.
6)
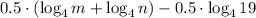
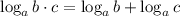
7)
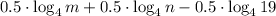 Distributive property/Result.
Distributive property/Result.
 is equivalent to
is equivalent to
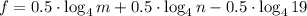 .
.