Question

Please help with this two part question (Calculus)^^

Answer 1

1) -0.016 pounds per square inch per cubic inch.

2)
`\displaystyle V'(P)=-(800)/(P^2)`

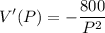
Explanation:

We are given the equation
`PV=800`.

Part A)

We want to determine the average rate of change of P as V increases from 200 cubic inches to 250 cubic inches.

To find the average rate of change between two points, we find the slope between them.

Rewrite the given equation as a function of V:

`\displaystyle P(V)=(800)/(V)`

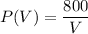
Hence, the average rate of change for V = 200 and V = 250 is:

`\displaystyle \begin{aligned} m &= (P(250) - P(200))/(250 - 200) \\ \\ & = (3.2 - 4)/(250 - 200) \\ \\ & = -0.016\end{aligned}`

Therefore, the average rate of change is -0.016 pounds per square inch per cubic inch.

Part B)

We want to express V as a function of P. This can be done through simple division:

`\displaystyle V(P)=(800)/(P)`

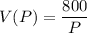
We want to show that the instantaneous change of V with respect to P is inversely proportional to the square of P. So, let's take the derivative of both sides with respect to P:

`\displaystyle (d)/(dP)\left[V(P)\right]=(d)/(dP)\left[(800)/(P)\right]`

Differentiate. Note that 1/P is equivalent to P⁻¹. This allows for a simple Power Rule:

`\displaystyle \begin{aligned} V'(P) & = 800(d)/(dP)\left[ P^(-1)\right] \\ \\ & = -800(P^(-2)) \\ \\ & = -(800)/(P^2)\end{aligned}`

Therefore, the instantaneous change of V is indeed inversely proportional to the square of P.