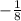Answer:
cosФ =
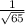 , sinФ =
, sinФ =
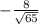 , tanФ = -8, secФ =
, tanФ = -8, secФ =
 , cscФ =
, cscФ =
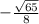 , cotФ =
, cotФ =
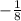
Explanation:
If a point (x, y) lies on the terminal side of angle Ф in standard position, then the six trigonometry functions are:
- cosФ =
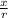
- sinФ =

- tanФ =
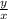
- secФ =
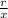
- cscФ =

- cotФ =

- Where r =
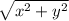 (the length of the terminal side from the origin to point (x, y)
(the length of the terminal side from the origin to point (x, y)
- You should find the quadrant of (x, y) to adjust the sign of each function
∵ Point (1, -8) lies on the terminal side of angle Ф in standard position
∵ x is positive and y is negative
→ That means the point lies on the 4th quadrant
∴ Angle Ф is on the 4th quadrant
∵ In the 4th quadrant cosФ and secФ only have positive values
∴ sinФ, secФ, tanФ, and cotФ have negative values
→ let us find r
∵ r =
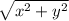
∵ x = 1 and y = -8
∴ r =

→ Use the rules above to find the six trigonometric functions of Ф
∵ cosФ =
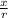
∴ cosФ =
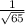
∵ sinФ =

∴ sinФ =
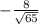
∵ tanФ =
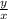
∴ tanФ =
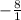 = -8
= -8
∵ secФ =
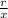
∴ secФ =
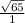 =
=

∵ cscФ =

∴ cscФ =
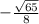
∵ cotФ =

∴ cotФ =