Question

How to find the perimeter of the triangle

Answer 1

A. 26.2

Explanation:

To find the perimeter of the triangle, you have to find the distances of all three lines and add them up.

Line AB

Let's start off by finding the distance of line AB.

We will use the formula,
`d = \sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`.

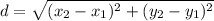Point A is (-2,5) and Point B is (4,-3).

To substitute the values, it will get to
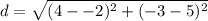`d = \sqrt{(4--2)^(2)+(-3-5)^(2)}` which in other words is
`d = \sqrt{(4+2)^(2)+(-3-5)^(2)}`.

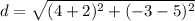Now we have to solve the parenthesis to get
`d = \sqrt{(6)^(2)+(-8)^(2)}`.

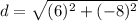Now we have to solve the exponents which would get to
`d = √(36+64)`.

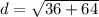Now we have to simplify the square root to
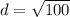`d = √(100)`. In other words, that is
`d = 10`.

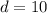Line AB = 10

Line BC

Now let's find the distance of line BC.

We will use the same formula,
`d = \sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`.

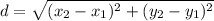Point B is (4,-3) and Point C is (0,-6).

To substitute the values, it will get to
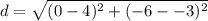`d = \sqrt{(0-4)^(2)+(-6--3)^(2)}` which in other words is
`d = \sqrt{(0-4)^(2)+(-6+3)^(2)}`.

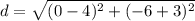Now we have to solve the parentheses to get
`d = \sqrt{(-4)^(2)+(-3)^(2)}`.

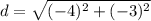Now we have to solve the exponents which would get to
`d = √(16+9)`.

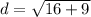Now we have to simplify the square root to
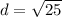`d = √(25)`. In other words, that is
`d = 5`.

Line BC = 5.

Line AC

Now let's fine the distance of line AC.

We will use the same formula,
`d = \sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}`.

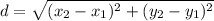Point A is (-2,5) and Point C is (0,-6).

To substitute the values, it will get to
`d = \sqrt{(0--2)^(2)+(-6-5)^(2)}` which in other words is
`d = \sqrt{(0+2)^(2)+(-6-5)^(2)}`.

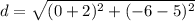Now we have to solve the parentheses to get
`d = \sqrt{(2)^(2)+(-11)^(2)}`.

Now we have to solve the exponents which would get to
`d = √(4+121)`.

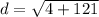Now we have to simplify the square root to
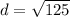`d = √(125)`. In other words, that is
`d = 5√(5)`. To round that,
`d = 11.2`.

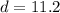Line AC = 11.2.

Perimeter of Triangle ABC

Perimeter of Triangle ABC = Line AB + Line BC + Line AC.

Perimeter of Triangle ABC = 10 + 5 + 11.2

Perimeter of Triangle ABC = 26.2

Hope this helped! If not, please let me know <3