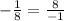Answer:
The product of
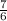 and
and
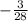 is
is
 . The reciprocal is
. The reciprocal is
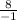 .
.
Explanation:
We have to find the product of
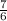 and
and
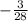 before we find the reciprocal.
before we find the reciprocal.
Before we do this though, we need to review a few words and their definitions.
First, the reciprocal of a fraction is when the numerator becomes denominator and the denominator becomes numerator.
Now we're ready to solve
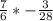 :
:
Step 1: Use this rule:
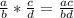 .
.

Step 2: Simplify 7 × - 3 to - 21.
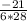
Step 3: Simplify 6 × 28 to 168.
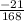
Step 4: Move the negative sign to the left.
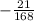
Step 5: Simplify
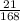 to
to
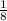 .
.

Now that we've found the product, we now must find the reciprocal.
Now using what we know and the process to find the reciprocal.
We can use that knowledge to find it: