Question

In a test of a printed circuit board using a random test pattern, an array of 14 bits is equally likely to be 0 or 1. Assume the bits are independent.

(a) What is the probability that all bits are 1s? Round your answer to six decimal places (e.g. 98.765432). Enter your answer in accordance to the item a) of the question statement
(b) What is the probability that all bits are 0s? Round your answer to six decimal places (e.g. 98.765432). Enter your answer in accordance to the item b) of the question statement
(c) What is the probability that exactly 7 bits are 1s and 7 bits are 0s? Round your answer to three decimal places (e.g. 98.765). Enter your answer in accordance to the item c) of the question statement

Answer 1

(a) 0.000061

(b) 0.000061

(c) 0.209

Explanation:

An array of 14 bits is equally likely to be 0 or 1.

That is, P (0) = P (1) = 0.50.

(a)

Compute the probability that all bits are 1s as follows:

`P(\text{All bits are 1s})=[P(1)]^(14)` ∵ the bits are independent

`=(0.50)^(14)\\=0.00006103515625\\\approx 0.000061`

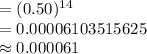
Thus, the probability that all bits are 1s is 0.000061.

(b)

Compute the probability that all bits are 0s as follows:

`P(\text{All bits are 0s})=[P(0)]^(14)` ∵ the bits are independent

`=(0.50)^(14)\\=0.00006103515625\\\approx 0.000061`

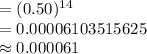
Thus, the probability that all bits are 0s is 0.000061.

(c)

Compute the probability that exactly 7 bits are 1s and 7 bits are 0s as follows:

Define X as the number of bits that 1s.

Then the random variable X will follows a binomial distribution with parameters n = 14 and p = 0.50.

The value of P (X = 7) is:

`P(X=7)={14\choose 7}(0.50)^(7)(1-0.50)^(14-7)`

`=(14!)/(7!* 7!)* (0.50)^(14)\\\\=3432* 0.000061\\\\=0.209352\\\\\approx 0.209`

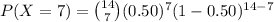
Thus, the probability that exactly 7 bits are 1s and 7 bits are 0s is 0.209.