Question

given the weekly demand curve of a local wine producer is p= 50-0.1q, and that the total cost function is c= 1500+ 10q, where q bottles are produced each day and sold at a price of $p per unit. a)Express the weekly profit as a function of price.b) at what price must a bottle of wine be sold to realise maximum profit. c) what is the maximum profit that ca be made by the producer

Answer 1

a)the weekly profit as a function of price is
`P=-10 p^2 + 600 p - 6500`

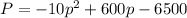
b) a bottle of wine be sold at $30 to realise maximum profit

c) the maximum profit that can be made by the producer is $2500

Explanation:

The weekly demand curve of a local wine producer is p= 50-0.1q

p = price

q = quantity

Revenue function R =Price \times Quantity

R=(50-0.1q)q

`R=50q-0.1q^2`

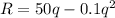
Cost function: c= 1500+ 10q

Profit function=R(x)-C(x)

Profit function=
`50q-0.1q^2-1500-10q`

Profit function=
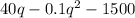`40q-0.1q^2-1500` ----1

We have q = 500 - 10 p using p = 50 − 0.1q

`P=-0.1 (500 - 10 p)^2 + 40 (500 - 10 p)- 1500\\P= -10 p^2 + 600 p - 6500`

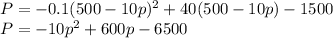
General quadratic equation:
`ax^2+bx+c=0`

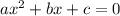
On comparing

a = -0.1 , b = 40 , c = -1500

Maximum Profit is at q =
`(-b)/(2a)=(-40)/(2(-0.1))=200`

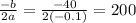
To find price must a bottle of wine be sold to realise maximum profit

p= 50-0.1q

p= 50-0.1(200)=30

Substitute the value of q in profit function(1) get the maximum profit

So, Profit function=
`40\left(200\right)-0.1\left(200\right)^(2)-1500=2500`

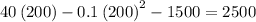
Hence

a)the weekly profit as a function of price is
`P=-10 p^2 + 600 p - 6500`

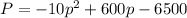
b) a bottle of wine be sold at $30 to realise maximum profit

c) the maximum profit that can be made by the producer is $2500