Question

A rectangle's length, f(x), is 2 more than three times a unit length, x, and its width, g(x), is twice the unit length, x. Combine functions f(x) and g(x) to get h(x). Which is h(x) written in the simplest form? H(x) = 5x + 2 h(x) = 6x + 2 h(x) = 6x2 + 2 h(x) = 6x2 + 4x

Answer 1

h(x) = 6x^2 + 4x

Explanation:

Got it right on lesson.

Answer 2

`h(x)=6x^2+4x`

Explanation:

As the rectangle's length, f(x), is 2 more than three times a unit length, x, so,

f(x)=3x+2

As the rectangle's width, g(x), is twice the unit length, x, so,

g(x)=2x.

The length and width of the rectangle are related to the area and the perimeter of the rectangle. So, the length, f(x), and the width, g(x), can be combined to give the area or perimeter, h(x).

So, h(x) might be the area or the perimeter of the rectangle.

If h(x) is the area, then

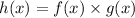`h(x)=f(x) * g(x)` [as area=lenght x width]

`\Rightarrow h(x)=(3x+2)* 2x`

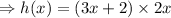
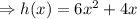`\Rightarrow h(x)=6x^2+4x` (this is in the given options)

If h(x) is the perimeter, then

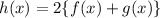`h(x)=2\{f(x) + g(x)\}` [as perimeter=2(lenght + width)]

`\Rightarrow h(x)=2\{(3x+2)+ 2x\}`

`\Rightarrow h(x)=2(5x+2)`

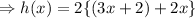
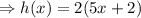
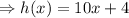`\Rightarrow h(x)=10x+4` (not in the given options)

So, from the given options
`h(x)=6x^2+4x` is correct.