Question

The sum of all the terms in an infinite geometric sequence is 81 and the sum

of all terms starting from the third is 9. What is the second term in the sequence?

Answer 1

Step (1)

We know that the sum of all the terms in an infinite geometric sequence finding from following equation whenever |q| < 1 .

q = magnitude

`s( \infty ) = (t(1))/(1 - q) \\`

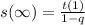
So :

`s( \infty ) = (t(1))/(1 - q) \\`

`81 = (t(1))/(1 - q) \\`

`81(1 - q) = t(1)`

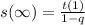
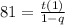
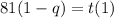
Remember it I'll use it again.

_________________________________

Step (2)

We know that the sum of the n first terms of a geometric sequence finding from following equation.

`s(n) = \frac{t(1) * (1 - {q})^(n) }{1 - q} \\`

_________________________________

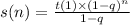
Sum of all terms starting from the third is 9.

So :

`s(2) + s(3 - \infty ) = 81`

`s(2) + 9 = 81`

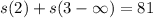
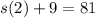
Sides minus 9

`s(2) = 81 - 9`

`s(2) = 72`

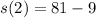
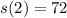
So :

`t(1) + t(2) = 72`

`t(1) + t(1) * q = 72`

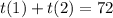
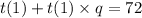
Factoring t(1)

`t(1) * (1 + q) = 72`

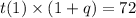
We have found t(1) = 81 ( 1 - q ) in step (1).

So :

`81(1 - q)(1 + q) = 72`

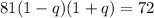
Divided sides by 81

`(1 - q)(1 + q) = (72)/(81) \\`

`(1 - q)( 1 + q) = (8)/(9) \\`

`1 - {q}^(2) = (8)/(9) \\`

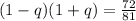
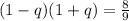
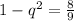
Subtract sides minus -1

`- {q}^(2) = (8)/(9) - 1 \\`

`- {q}^(2) = (8)/(9) - (9)/(9) \\`

`- {q}^(2) = - (1)/(9) \\`

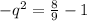
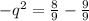
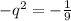
Negatives simplifies

`{q}^(2) = (1)/(9) \\`

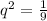
Radical sides

`q = + (1)/(3) \\ q = - (1)/(3)`

_________________________________

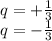
Step (4)

If q = 1/3 :

`81(1 - q) = t(1)`

`81(1 - (1)/(3)) = t(1) \\`

`81( (2)/(3)) = t(1) \\`

`t(1) = 27 * 2`

`t(1) = 54`

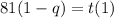
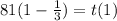
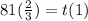
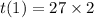
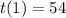
So :

`t(2) = t(1) * q`

`t(2) = 54 * (1)/(3) \\`

`t(2) = 18`

°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°

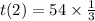
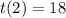
If q = - 1/3 :

`81(1 - q) = t(1)`

`81(1 - ( - (1)/(3))) = t(1) \\`

`81(1 + (1)/(3)) = t(1) \\`

`81( (4)/(3)) = t(1) \\`

`t(1) = 27 * 4`

`t(1) = 108`

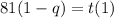
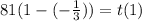
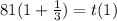
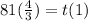
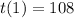
So :

`t(2) = t(1) * q`

`t(2) = 108 * - (1)/(3) \\`

`t(2) = - 36`

_________________________________

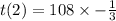
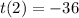
And we're done.

Thanks for watching buddy good luck.

♥️♥️♥️♥️♥️