Question

Prove that the following lines are parallel to each other.

3x+4y-7=0 and 6x+8y-11=0

(plzz do in process )
​

Answer 1

Yes, they are paralle.

Explanation:

Answer 2

Explanation:

Hey there!

Here;

The equations are:

3x + 4y - 7 = 0.............(I)

6x + 8y -11 = 0.........(ii)

Let's simply work with this.

From equation (I)

`slope(m) = ( - coeff.of \: x)/(coeff.of \: y)`

`m1 = ( - 3)/(4)`

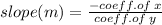
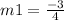
From equation (ii)

`slope(m2) = ( - coeff. \: of \: x)/(coeff. \: of \: y)`

`m2 = ( - 6)/(8)`

`m2 = ( - 3)/(4)`

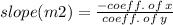
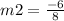
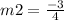
As per the condition of parallel lines;

M1 = M2

-3/4 = -3/4. (true)

Therefore, the lines are parallel to eachother.

Hope it helps...