Question

Find the x-values at which f is not continuous.
f(x) = tan(πx/2)

Answer 1

`x\\eq 1+2n,n\in\mathbb{Z}`

Explanation:

Remember that for the tangent parent function, it has infinite discontinuities (vertical asymptotes) on:

`f(x)=\tan(x), \\\text{Where }x\\eq(\pi)/(2)+n\pi, n\in\mathbb{Z}`

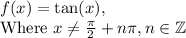
Here, we have:

`f(x)=\tan((\pi x)/(2))`

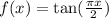
So, we can set the expression inside the tangent to equal our parent domain restriction. This yields:

`(\pi x)/(2)\\eq(\pi)/(2)+n\pi`

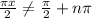
Solve for x. Multiply both sides by 2:

`\pi x\\eq \pi+2n\pi`

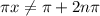
Divide both sides by π:

`x\\eq 1+2n, n\in\mathbb{Z}`

Therefore, for the function
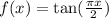`f(x)=\tan((\pi x)/(2))`, it is not continuous for all Xs
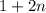`1+2n` where
`n\in\mathbb{Z}`