Question

Determine if this series converges or diverges. Find the sum if possible. 250, 50, 10...

Answer 1

50

Explanation:

Answer 2

312.5

Explanation:

We have the series: 250, 50, 10...

As we can see, each subsequent term gets smaller and smaller. Eventually, it will be infinitesimally small. So, our series converges.

We can also see this from our common ratio. Each term is 1/5 of the previous term. Since our r 1/5 is less than 1, our series will converge.

Since it converges, we can indeed find our sum. First, we can write our series using summation. This will be:

`\displaystyle{\sum_(n=0)^(\infty) 250((1)/(5))^n }`

We can use the following infinite geometric series formula:

`\displaystyle{\sum_(n=0)^(\infty) ar^n=(a)/(1-r)`

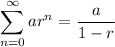
So, let's substitute 250 for a and 1/5 for r. This yields:

`\displaystyle{\sum_(n=0)^(\infty) 250((1)/(5))^n }=(250)/(1-(1)/(5))`

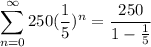
Subtract:

`\displaystyle{\sum_(n=0)^(\infty) 250((1)/(5))^n }=(250)/((4)/(5))`

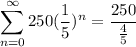
Divide. So, our series converges to:

`\displaystyle{\sum_(n=0)^(\infty) 250((1)/(5))^n }=312.5`

And we're done!