Question

A magician performs in a room with a ceiling, which is 2.70 m above his hands. He throws a ball upwards such that it reaches the ceiling with zero speed. Calculate the initial speed of the ball and the time it takes for it to reach the ceiling. A magician performs in a room with a ceiling, which is 2.70 m above his hands. He throws a ball upwards such that it reaches the ceiling with zero speed. Calculate the initial speed of the ball and the time it takes for it to reach the ceiling.

Answer 1

a) v = 7.28 m/s

b) t = 0.74 s

Step-by-step explanation:

a) The initial speed of the ball can be calculated using the following equation:

`V_(f)^(2) = V_(0)^(2) - 2gh`

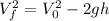
Where:

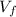`V_(f)` is the final speed = 0

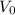`V_(0)` is the initial speed =?

g: is the gravity = 9.81 m/s²

h: is the height = 2.70 m

`V_(0) = √(2gh) = \sqrt{2*9.81 m/s^(2)*2.70 m} = 7.28 m/s`

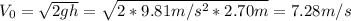
Hence, the initial speed of the ball is 7.28 m/s.

b) To find the time that takes the balls to reach the ceiling we can use the next equation:

`V_(f) = V_(0) - gt`

`t = (V_(0) - V_(f))/(g) = (7.28 m/s)/(9.81 m/s^(2)) = 0.74 s`

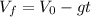
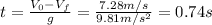
Therefore, the time it takes for the ball to reach the ceiling is 0.74 s.

I hope it helps you!