Question

Jamie needs to build a fence around his garden, as illustrated by polygon ABCDEF on the coordinate grid below. If each unit represents one yard, what is the total length of Jamie's fence in yards?

(72 POINTS)
Please don't just answer for points if you know the answer you know the answer

(Homework assignment worth a test grade so need someone who knows their stuff)

Answer 1

C. 26 yards

Explanation:

Jamie's fence total length = perimeter of the polygon

Perimeter of the polygon = AB + BC + CD + DE + EF + FA

AB, FA and DE can be worked accordingly as shown below:

AB = |-5 - 0| = 5 units

FA = |5 - 2| = 3 units

DE = |1 -(-2)| = 3 units

BC, CD, and EF can be calculated using the formula
`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

Distance between B(0, 5) and C(4, 2):

`BC = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

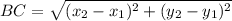
Let,

`B(0, 5) = (x_1, y_1)`

`C(4, 2) = (x_2, y_2)`

`BC = √((4 - 0)^2 + (2 - 5)^2)`

`BC = √((4)^2 + (-3)^2)`

`BC = √(16 + 9) = √(25)`

`BC = 5 units`

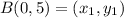
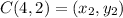
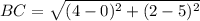
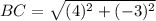
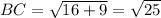
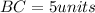
Distance between C(4, 2) and D(1, -2)

`CD = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

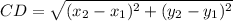
Let,

`C(4, 2) = (x_1, y_1)`

`D(1, -2) = (x_2, y_2)`

`CD = √((1 - 4)^2 + (-2 - 2)^2)`

`CD = √((-3)^2 + (-4)^2)`

`CD = √(9 + 16) = √(25)`

`CD = 5 units`

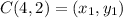
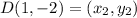
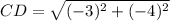
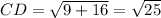
Distance between E(-2, -2) and F(-5, 2):

`EF = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

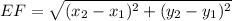
Let,

`E(-2, -2) = (x_1, y_1)`

`F(-5, 2) = (x_2, y_2)`

`EF = √((-5 -(-2))^2 + (2 -(-2))^2)`

`EF = √((-3)^2 + (4)^2)`

`EF = √(9 + 16) = √(25)`

`EF = 5 units`

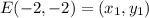
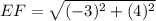
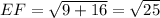
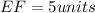
Total length of the wall in yards = 5 + 5 + 5 + 3 + 5 + 3 = 26 yards