Answer:
As
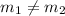 , we conclude that both lines are not parallel to each other.
, we conclude that both lines are not parallel to each other.
Step-by-step explanation:
We must remember from Analytic Geometry that two lines are parallel to each other if and only if both lines have the same slope. We may calculate each slope by knowing each pair of distinct points passing through each segment:
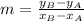
Where:
 - Slope, dimensionless.
- Slope, dimensionless.
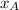 ,
,
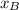 - Initial and final x-Components, dimensionless.
- Initial and final x-Components, dimensionless.
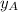 ,
,
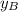 - Initial and final y-Components, dimensionless.
- Initial and final y-Components, dimensionless.
If we know that
 ,
,
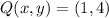 ,
,
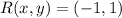 and
and
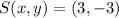 , then:
, then:
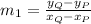

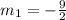

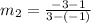
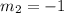
As
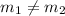 , we conclude that both lines are not parallel to each other.
, we conclude that both lines are not parallel to each other.