Question

Consider the function f ( ) round( ) x x  , which rounds the input, x, to the nearest integer. Is this function

one-to-one? Explain or justify your answer.

please help

Answer 1

The function is not one-to-one

Explanation:

Required

Determine if
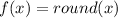`f(x) = round(x)` is one-to-one

To answer this question, we need to make use of illustrating values of x.

Take x = 6.7

This implies that:

`f(6.7) = round(6.7)`

`f(6.7) = 7`

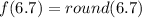
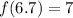
Also, Take x = 6.8

`f(6.8) = round(6.8)`

`f(6.8) = 7`

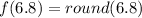
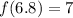
Notice that the above values of x give the same resulting value of f(x).

If you also take x = 7.4

`f(7.4) = round(7.4)`

`f(7.4) = 7`

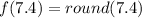
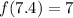
This also gives the same value as the (2) illustration previously used

With these illustrations, we've seen that f(x) has the tendency to have more than one values for different values of x.

Hence:

The function is not one-to-one