Question

A data set lists weights​ (lb) of plastic discarded by households. The highest weight is 5.29 ​lb, the mean of all of the weights is x=1.995 ​lb, and the standard deviation of the weights is s=1.305 lb. a. What is the difference between the weight of 5.29 lb and the mean of the​ weights? b. How many standard deviations is that​ [the difference found in part​ (a)]? c. Convert the weight of 5.29 lb to a z score. d. If we consider weights that convert to z scores between −2 and 2 to be neither significantly low nor significantly​ high, is the weight of 5.29 lb​ significant?

Answer 1

Follows are the solution to this question:

Explanation:

In point a:

The weight difference between 5.29 lb and the weighted mean:

`=5.29-1.995 \\\\=3.295`

In point b:

The number of standard deviation:

`=(3.295)/(1.305) \\\\ =2.52`

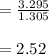
In point c:

`z score= (x- \mu)/(\sigma)\\\\`

`=( 1.995- 5.29)/(1.305)\\\\=(-3.295)/(1.305)\\\\= - 2.52`

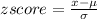
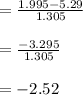
In point d:

No, since (-2, 2) included with the Zero is the z score and for weight is 5.29.