Question

Suppose an employee is suspected of having used an illegal drug and is given two tests that operate independently of each other. Test A has probability 0.91 of being positive if the illegal drug has been used. Test B has probability 0.88 of being positive if the illegal drug has been used. The company requires that an employee, Al Capone, take and pass both tests to keep his job. Assume that Al has, in fact, been using the illegal drug. What is the probability that neither test is positive (and thus Al gets to keep his job)

Answer 1

The probability that neither test is positive

P(A⁻ ∩ B⁻ ) = 0.0108

Explanation:

Step(i) :-

Given the two tests are independently

Test A has probability 0.91 of being positive if the illegal drug has been used

P(A) = 0.91

Test B has probability 0.88 of being positive if the illegal drug has been used

P(B) = 0.88

If events are independently then ,

`P(A n B) = P(A) P(B)`

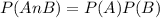
Step(ii):-

The probability that neither test is positive (and thus Al gets to keep his job)

`P(A^(-) n B^(-) ) = P(A^(-) ) P(B^(-) )`

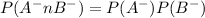
P(A⁻ ∩ B⁻ ) = P(A⁻ ) P(B⁻ )

= ( 1- P(A) ) ( 1 - P(B))

= (1 - 0.91 ) ( 1 - 0.88 )

= (0.09) (0.12)

= 0.0108

The probability that neither test is positive

P(A⁻ ∩ B⁻ ) = 0.0108