These triangles are scaled copies of each other. For each pair of triangles listed, the area of the second triangle is how many times larger than the area of the first?

Question

asked Jan 6, 2021 100k views

1 Answer

Sihoon Kim · Answer 1 · 2021-01-12T10:00:25+0000

Answer/Step-by-step explanation:

Recall: the ratio of the areas of two similar figures = the square of the ratio of the corresponding sides of the similar figures.

This will give us the scale factor.

The scale factor indicates how many times larger the second triangle is than the area of the first.

Let's find how many times larger is the area of the second triangle is to the first:

1. ∆ G And ∆ F

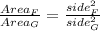
(Area_(F))/(Area_(G)) = (side_(F)^2)/(side_(G)^2)

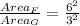
(Area_(F))/(Area_(G)) = (6^2)/(3^2)

= (36)/(9) = 4

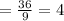
∆F is 4 times larger than ∆G

2. ∆ G And ∆ B

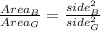
(Area_(B))/(Area_(G)) = (side_(B)^2)/(side_(G)^2)

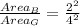
(Area_(B))/(Area_(G)) = (2^2)/(4^2)

= (4)/(16) = 0.25

∆B is 0.25 times ∆G

3. ∆ B And ∆ F

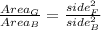
(Area_(G))/(Area_(B)) = (side_(F)^2)/(side_(B)^2)

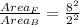
(Area_(F))/(Area_(B)) = (8^2)/(2^2)

= (64)/(4) = 4

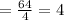
∆F is 16 times larger than ∆B

4. ∆ F And ∆ H

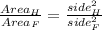
(Area_(H))/(Area_(F)) = (side_(H)^2)/(side_(F)^2)}

(Area_(H))/(Area_(F)) = (2^2)/(6^2)

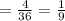
= (4)/(36) = (1)/(9)

∆H is ⅑ times ∆F

5. ∆ G And ∆ H

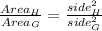
(Area_(H))/(Area_(G)) = (side_(H)^2)/(side_(G)^2)

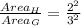
(Area_(H))/(Area_(G)) = (2^2)/(3^2)

= (4)/(9)

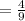
∆G is 4/9 times ∆G

6. ∆ H And ∆ B

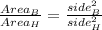
(Area_(B))/(Area_(H)) = (side_(B)^2)/(side_(H)^2)

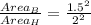
(Area_(B))/(Area_(H)) = (1.5^2)/(2^2)

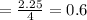= (2.25)/(4) = 0.6 (nearest tenth)

∆B is 0.6 times ∆H