Question

50 points! I understand A. and B. but I would really appreciate help with C.

Answer 1

`51.72\text{ cells per hour}`

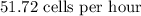
Explanation:

So, the function, P(t), represents the number of cells after t hours.

This means that the derivative, P'(t), represents the instantaneous rate of change (in cells per hour) at a certain point t.

C)

So, we are given that the quadratic curve of the trend is the function:

`P(t)=6.10t^2-9.28t+16.43`

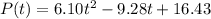
To find the instanteous rate of growth at t=5 hours, we must first differentiate the function. So, differentiate with respect to t:

`(d)/(dt)[P(t)]=(d)/(dt)[6.10t^2-9.28t+16.43]`

Expand:

`P'(t)=(d)/(dt)[6.10t^2]+(d)/(dt)[-9.28t]+(d)/(dt)[16.43]`

Move the constant to the front using the constant multiple rule. The derivative of a constant is 0. So:

`P'(t)=6.10(d)/(dt)[t^2]-9.28(d)/(dt)[t]`

Differentiate. Use the power rule:

`P'(t)=6.10(2t)-9.28(1)`

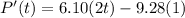
Simplify:

`P'(t)=12.20t-9.28`

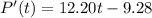
So, to find the instantaneous rate of growth at t=5, substitute 5 into our differentiated function:

`P'(5)=12.20(5)-9.28`

Multiply:

`P'(5)=61-9.28`

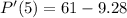
Subtract:

`P'(5)=51.72`

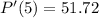
This tells us that at exactly t=5, the rate of growth is 51.72 cells per hour.

And we're done!