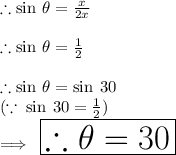Question

Tthe diagonals of a rectangle are twice as long as the shorter sides. calculate the angle between a diagonal and a short side.

Answer 1

30°

Explanation:

Let the length of shorter side of rectangle be x units.

Therefore, length of diagonal = 2x

In order to calculate the angle between a diagonal and a short side, we need to find the sin ratio of shorter side and diagonal of rectangle.

Let the measure of angle formed between shorter side and diagonal be
`\theta`.

`\therefore \sin \: \theta = (x)/(2x) \\ \\ \therefore \sin \: \theta = (1)/(2) \\ \\\therefore\sin \: \theta = \sin \: 30 \degree \\ ( \because \: \sin \: 30 \degree = (1)/(2)) \\ \implies \: \huge \red{ \boxed{\therefore\theta = 30 \degree }}`