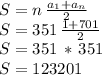Question

Use S = n^2 to find the sum of 1 + 3 + 5 + . . . + 701.

Answer 1

123201

Explanation:

This is an arithmetic sequence of common difference 2 and starting value 1,

So we can use the formula for an arithmetic sequence if we know what is the order of the last term.

Then first use the formula for the nth term to find "n":

`a_n=a_1+(n-1)d`

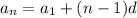
where d = 2, first term = 1 and last term = 701

`a_n=a_1+(n-1)d\\701=1+(n-1)*2\\700=(n-1)*2\\350=n-1\\n = 351`

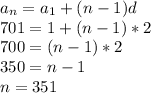
Knowing this, we can estimate the partial sum:

`S=n\,(a_1+a_n)/(2) \\S=351\,(1+701)/(2) \\S=351\,*\,351\\S = 123201`