Question

Universal Foods issued 10% bonds, dated January 1, with a face amount of $260 million on January 1, 2018. The bonds mature on December 31, 2037 (20 years). The market rate of interest for similar issues was 12%. Interest is paid semiannually on June 30 and December 31. Universal uses the straight-line method. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Required: 1. Determine the price of the bonds at January 1, 2018. 2. to 4. Prepare the journal entry to record their issuance by Universal Foods on January 1, 2018, interest on June 30, 2018 and interest on December 31, 2025.

Answer 1

The bonds were issued at $220,879,628.13

This is lower than the face value to compensate for the lower coupon payment.

cash 220,879,628.13 debit

discount on BP 39,120,371.87 debit

bonds payable 260,000,000 credit

--to record the issuance of the bonds--

Interest expense 13,252,777.69 debit

Discoun on BP 252,777.69 credit

cash 13,000,000 credit

--to record the first interest payment--

Interest expense 13,267,944.35 debit

Discount on BP 267,944.35 credit

Cash 13,000,000 credit

--to record second interest payment--

Interest expense 13,539,156.67 debit

Discount on BP 539,156.67 credit

cash 13,000,000.00 credit

--to record Dec 31st, 2025 payment--

Step-by-step explanation:

To determinate the price we will solve for the present value of the coupon payment and maturity at the market rate of %12

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

Coupon payment:

260,000,000 x 10% x 1/2 =13,000,000.000

time 20 years x 2 payment per year 40

yield to maturity 12% / 2 = 6%

`13000000 * (1-(1+0.06)^(-40) )/(0.06) = PV\\`

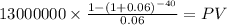
PV $195,601,859.3298

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 260,000,000.00

time 40.00

rate 0.06

`(260000000)/((1 + 0.06)^(40) ) = PV`

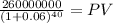
PV 25,277,768.80

PV c $195,601,859.3298

PV m $25,277,768.8042

Total $220,879,628.1340

For the journal entries, we will multiply this current market price of the bonds by the market rate (YTM) the difference between this and the actual cash obligation generate by the bond is the amortization of the discount.

first interest payment

$220,879,628.13 x 6% = 13,252,777.69

less actual cash outlay: 13,000,000

amortization 252,777.69

second interest payment

($220,879,628.13- $252,777.69) x 6% = 13,267,944.35

less actual cash outlay: 13,000,000.00

amortization 267,944.35

December 31st, 2025:

This will be payment 14th

after building the schedule until that date we got: