Question

LA plane is trying to travel 250 miles at a bearing of 20° E of S, however, it ends 230 miles away from the

starting point in the direction of 35° E of South. How far did the wind push the plane and in what direction?

Answer 1

The wind pushed the plane
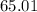`65.01` miles in the direction of
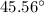`45.56 ^(\circ)` East of North with respect to the destination point.

Explanation:

Let origin, O, br the starting point and point D be the destination at 250 miles at a bearing of 20° E of S, but due to wind let D' be the actual position of the plane at 230 miles away from the starting point in the direction of 35° E of South as shown in the figure.

So, we have |OD|=250 miles and |OD'|=230 miles.

Vector
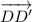`\overrightarrow{DD'}` is the displacement vector of the plane pushed by the wind.

From figure, the magnitude of the required displacement vector is

`|DD'|=√(|AB|^2+|PQ|^2)\;\cdots(i)`

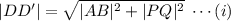
and the direction is
`\alpha` east of north as shown in the figure,

`\tan \alpha=(|PQ|)/(|AB|)\;\cdots(ii)`

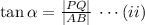
From the figure,

`|AB|=|OA-OB|`

`\Rightarrow |AB|=|OD\cos 20 ^(\circ)-OD'\cos 35 ^(\circ)|`

`\Rightarrow |AB|=|250\cos 20 ^(\circ)-230\cos 35 ^(\circ)|`

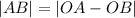
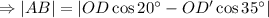
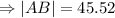`\Rightarrow |AB|=45.52` miles

Again,
`|PQ|=|OP-OQ|`

`\Rightarrow |PQ|=|OD\sin 20 ^(\circ)-OD'\sin 35 ^(\circ)|`

`\Rightarrow |PQ|=|250\sin 20 ^(\circ)-230\sin 35 ^(\circ)|`

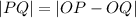
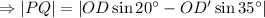
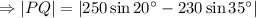
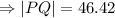`\Rightarrow |PQ|=46.42` miles

Now, from equations (i) and (ii), we have

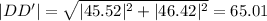`|DD'|=√(|45.52|^2+|46.42|^2)=65.01` miles, and

`\tan \alpha=(|46.42|)/(|45.52|)`

`\alpha=\tan^(-1)\left((|46.42|)/(|45.52|)\right)=45.56 ^(\circ)`

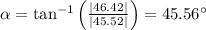
Hence, the wind pushed the plane
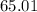`65.01` miles in the direction of
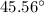`45.56 ^(\circ)` E astof North with respect to the destination point.