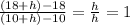Given f ( x ) = 1 x + 8 , find the average rate of change of f ( x ) on the interval [ 10 , 10 + h ] . Your answer will be an expression involving h .

Question

asked Oct 9, 2021 119k views

1 Answer

Anton Khodak · Answer 1 · 2021-10-14T11:11:45+0000

Answer:

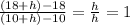
((18 + h) - 18)/((10 + h) - 10) = (h)/(h) = 1

Explanation:

Given: f(x) = x + 8

Interval: [10, 10 + h]

The function f(x) is an equation of a straight line and can also be expressed as;

y = x + 8

*The slope in this case is equal to 1.

∴ When x = 10 , y = 10 + 8 = 18

and,

When x = 10 + h , y = (10 + h) + 8 = 18 + h

Average rate of change is equivalent to the slope of the line but we should express it in terms of h.

So we are finding the rate of change from point (10, 18) to point (10 + h, 18 + h)

Slope = change in y ÷ change in x

i.e

Average rate of change or slope =
((18 + h) - 18)/((10 + h) - 10) = (h)/(h) = 1