Answer:
The arc-length is about 1.1953.
Explanation:
We are given the equation:
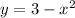
And we want to find the length of its arc from:
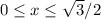
Recall that arc-length is given by the formula:
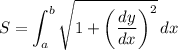
By differentiating and substituting into the arc-length formula, we will acquire:

To evaluate, we can use trigonometric substitution. Note that:
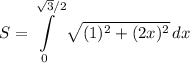
Since this is in the form a² + u², we will make the substitution u = atan(θ).
In this case, a = 1 and u = 2x. Thus:
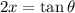
Differentiating both sides with respect to x:
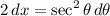
So:

Additionally, we must rewrite our bounds. Hence:

And:
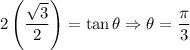
Thus:
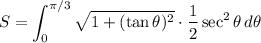
Simplify:
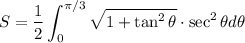
Using trigonometric identities:

Simplify:
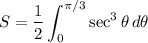
We can apply the reduction formula:
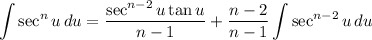
Hence:
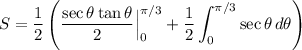
This is a common integral:
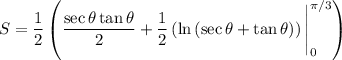
Evaluate. Hence:
![\displaystyle \begin{aligned} S = (1)/(2)\left[\left((\sec(\pi)/(3)\tan(\pi)/(3))/(2)+(1)/(2)\ln\left(\sec(\pi)/(3)+\tan(\pi)/(3)\right)\right) \\ - \left((\sec0\tan0)/(2)+(1)/(2)\ln\left(\sec 0 +\tan 0\right)\right)\right] \end{aligned}](https://img.qammunity.org/2021/formulas/mathematics/college/u46ebt60467drugzhurb8jyod8n4fqs9jz.png)
Evaluate:
![\displaystyle \begin{aligned} S &=(1)/(2) \left[ \left(((2)\left(√(3)\right))/(2) + (1)/(2)\ln \left(2 + √(3)\right) \right)-\left(((1)(0))/(2) + (1)/(2)\ln \left(1+0\right) \right) \right] \\ \\&= (1)/(2)\left(√(3) + (1)/(2) \ln \left(2+√(3)\right)\right) \\ \\ &\approx 1.1953 \end{aligned}](https://img.qammunity.org/2021/formulas/mathematics/college/bh1zu9c7398nls3eyy7hgsbrwp39fed6qd.png)
Thus, the length of the arc is about 1.1953 units.