Question

Determine which of these sequences is an arithmetic sequence. Then determine the explicit formula that would be used to define the nth term in the sequence.

Answer 1

6)

34, 43, 52, 61, ...

43-34 = 9; 52-43 = 9; 61-52 = 9

The difference between one term and the next is a constant so it is arithmetic sequence

first term: a = 34

difference: d = 9

so the formula:

`a_n=a+d(n-1)\\\\a_n=34+9(n-1)\\\\a_n = 34+9n-9\\\\\underline{a_n=9n+25}`

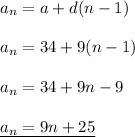
7)

10, 6, 2, -2, ...

6-10 = -4; 2-6 = -4; -2-2 = -4

The difference between one term and the next is a constant so it is arithmetic sequence

first term: a = 10

difference: d = -4

so the formula:

`a_n=a+d(n-1)\\\\a_n=10+(-4)(n-1)\\\\a_n = 10-4n+4\\\\\underline{a_n=-4n+14}`

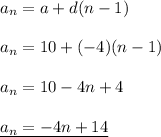
8)

-3, -10, -17, -24, ...

-10-(-3) = -7; -17-(-10) = -7; -24-(-17) = -7

The difference between one term and the next is a constant so it is arithmetic sequence

first term: a = -3

difference: d = -7

so the formula:

`a_n=a+d(n-1)\\\\a_n=-3+(-7)(n-1)\\\\a_n =-3-4n+7\\\\\underline{a_n=-7n+4}`

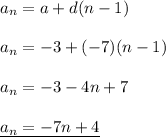
9)

7, 8.5, 10, 11.5, ...

8.5-7 = 1.5; 10-8.5 = 1.5; 11.5-10 = 1.5

The difference between one term and the next is a constant so it is arithmetic sequence

first term: a = 7

difference: d = 1.5

so the formula:

`a_n=a+d(n-1)\\\\a_n=7+1.5(n-1)\\\\a_n =7+1.5n-1.5\\\\\underline{a_n=1.5n+5.5}`

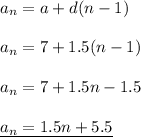
10)

30, 22¹/₂, 15, 7¹/₂, ...

22¹/₂-30 = -7¹/₂; 15-22¹/₂ = -7¹/₂; 7¹/₂-15 = -7¹/₂

The difference between one term and the next is a constant so it is arithmetic sequence

first term: a = 30

difference: d = -7¹/₂

so the formula:

`a_n=a+d(n-1)\\\\a_n=30+(-7\frac12)(n-1)\\\\a_n =30-7\frac12n+7\frac12\\\\ \underline{a_n=-7\frac12n+37\frac12}`