Solution:
Calculating the polled variance
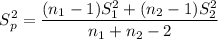
=
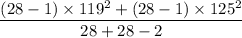
= 14893
Now we calculate the estimated standard error
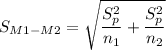
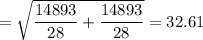
Thus , the 99 percent confidence interval is
=
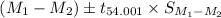
= 351 - 305 ± 2.660 x 32.6
= (46) ± 86.74
= (-40.74, 132.74)
Now the null hypothesis is :
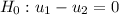
Against the alternative hypothesis
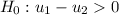
Computing the statistics ,
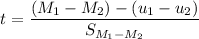
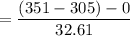
= 1.41