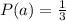Question

Problem 5 (4+4+4=12) We roll two fair 6-sided dice. Each one of the 36 possible outcomes is assumed to be equally likely. 1) Find the probability that doubles (i.e., having an equal number on the two dice) were rolled. 2) Given that the roll resulted in a sum of 4 or less, find the conditional probability that doubles were rolled. 3) Given that the two dice land on different numbers, find the conditional probability that at least one die is a 1.

Answer 1

1

`p(b) =  (1)/(6)`

2

`p(k) =  (1)/(3)`

3

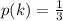
`P(a) = (1)/(3)`

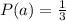
Explanation:

Generally when two fair 6-sided dice is rolled the doubles are

(1 1) , ( 2 2) , (3 3) , (4 4) , ( 5 5 ), (6 6)

The total outcome of doubles is N = 6

The total outcome of the rolling the two fair 6-sided dice is

n = 36

Generally the probability that doubles (i.e., having an equal number on the two dice) were rolled is mathematically evaluated as

`p(b) = (N)/(n)`

`p(b) = (6)/(36)`

`p(b) = (1)/(6)`

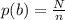
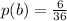
Generally when two fair 6-sided dice is rolled the outcome whose sum is 4 or less is

(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (3, 1)

Looking at this outcome we see that there are two doubles present

So

The conditional probability that doubles were rolled is mathematically represented as

`p(k) = (2)/(6)`

`p(k) = (1)/(3)`

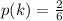
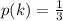
Generally when two fair 6-sided dice is rolled the number of outcomes that would land on different numbers is L = 30

And the number of outcomes that at least one die is a 1 is W = 10

So

The conditional probability that at least one die is a 1 is mathematically represented as

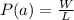
`P(a) = (W)/(L)`

=>
`P(a) = (10)/(30)`

=>
`P(a) = (1)/(3)`