Question

Find the measure of an interior angle of a regular polygon of 9 sides​

Answer 1

We know that, the sum of all angles of a polygon can be calculated by:

`(n - 2) * 180 \degree`

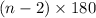
But in case of regular polygon, all the angles are equal. So, the measure of each angle can be found by dividing it by number of sides i.e n.

So, Value of each angle:

`((n - 2) * 180 \degree)/(n)`

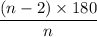
Given

• No. of sides of the regular polygon = 9

By using formula,

Measure of each interior angle:

`((9 - 2) * 180 \degree)/(9)`

`(7 * 180 \degree)/(9)`

`7 * 20 \degree`

`\boxed{ \red{ \bf{140 \degree}}}`

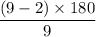
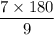
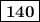
So, measure of each angle = 140°

And we are done !!

#CarryOnLearning

━━━━━━━━━━━━━━━━━━━━

Answer 2

The answer is

140°

Explanation:

An interior angle of a regular polygon can be found by using the formula

`((n - 2) * 180)/(n)`

where

n is the number of sides of the polygon

From the question the polygon has 9 sides that's n = 9

Substitute this value into the above formula and solve

We have

`((9 - 2) * 180)/(9) \\ \rarr \: (7 * 180)/(9) \\ \rarr \: (1260)/(9) \: \: \: \: \: \:`

We have the final answer as

140°

Hope this helps you