Question

Find the inverse of the given function.

Answer 1

The inverse is

`y =\sqrt{(((x-3)/(3)) ^(2)+5)/(2)}`

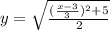
Explanation:

`y=3\sqrt{2x^(2) -5} + 3`

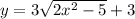
To find the inverse of the function interchange the terms that's x becomes y and y becomes x

We have

`x=3\sqrt{2y^(2)-5 }+3`

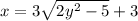
Now solve for y

Move 3 to the other side of the equation

`3\sqrt{2y^(2)-5 } = x-3`

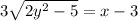
Divide both sides by 3

We have

`\sqrt{2y^(2)-5 } =(x-3)/(3)`

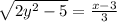
square both sides of the equation to remove the square root

That's

`2y^(2)-5 = ((x-3)/(3)) ^(2)`

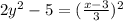
Move 5 to the other side of the equation

`2y^(2) = ((x-3)/(3)) ^(2)+5`

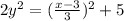
Divide both sides by 2

We have

`y^(2) = (((x-3)/(3)) ^(2)+5)/(2)`

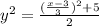
Find the square root of both sides

We have the final answer as

`y =\sqrt{(((x-3)/(3)) ^(2)+5)/(2)}`

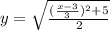
Hope this helps you