Solve the inequality x^2 -2x - 8 >0

Question

asked May 12, 2021 109k views

1 Answer

Wryte · Answer 1 · 2021-05-18T22:35:35+0000

Answer:

$x<-2\text{ or } x>4$

Explanation:

So we have the inequality:

x^2-2x-8>0

First, let's solve for the zeros of the function.

This is a quadratic, so we can factor. Let's ignore the inequality sign for now and pretend it is an equal sign. So:

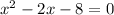
x^2-2x-8=0

Factor:

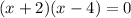
(x+2)(x-4)=0

Zero Product Property:

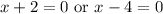
$x+2=0\text{ or } x-4=0$

Subtract 2 from both sides for the first equation and add 4 to both sides for the second:

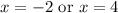
$x=-2\text{ or } x=4$

Therefore, our zeros are at (-2,0) and (4,0).

Now, since our leading coefficient is positive and we have a greater than symbol, this is an or inequality.

Since it's positive, it is all the value to the left and right of the zeros.

To see why this is, imagine the graph itself. It is going upwards and has roots at x=-2 and x=4.

Therefore, the graph is above 0 before x=-2 and after x=4. Between x=-2 and x=4, the graph is below 0.

Therefore, our solution is:

$x<-2\text{ or } x>4$