Question

N = 20

s = 18
H₀: σ² ≤ 384
H‎ₐ: σ₂ > 384

The null hypothesis is to be tested at the 5% level of significance. Give the critical value(s) from the table.
(no table is provided with the question)

A. 30.144
B. 31.410
C. 9.591 and 34.170
D. 8.907 and 32.852

Answer 1

A. 30.144

Explanation:

This is a Chi-Squared test

Given:

• 
  `n=20`
• 
  `s=18`
• 
  `\textsf{H}_0:\sigma^2=384`
• 
  `\textsf{H}_1:\sigma^2 > 384`
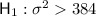
• The significance level is 5%, so
  `\alpha= 0.05`

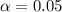
To use the Chi-Square distribution table, you need to know two values:

• Degrees of freedom = (n - 1)
• Significance level

Degrees of Freedom = n - 1 = 20 - 1 = 19

The significance level is 5%, so
`\alpha= 0.05`

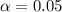
This is a one-tailed test since
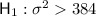`\textsf{H}_1:\sigma^2 > 384` so Upper tail area = 0.05

Reading from the table (attached), the critical value is: 30.144

(This means that we reject
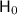`\textsf{H}_0` if the test statistic is greater than 30.144)