Answer:
The point on the line
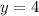 that is equidistant from points (0,1) and (5,6) is (2, 4).
that is equidistant from points (0,1) and (5,6) is (2, 4).
Explanation:
Let be
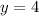 ,
,
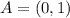 and
and
 . As we know that given function is a horizontal line, the condition of equidistance between that a point within that line and both points must be:
. As we know that given function is a horizontal line, the condition of equidistance between that a point within that line and both points must be:
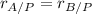
Where:
 - Distance of point A with respect to P.
- Distance of point A with respect to P.
 - Distance of point B with respect to P.
- Distance of point B with respect to P.
We expand this equivalence by Pythagorean Theorem:
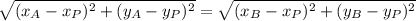
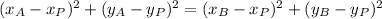
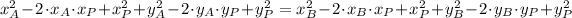
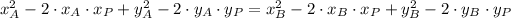
And we get this expression:

If we know that
 ,
,
 ,
,
 ,
,
 and
and
 , the expression is reduced to this:
, the expression is reduced to this:
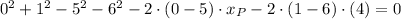
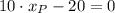
The remaining component of the point within the line is:
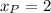
The point on the line
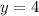 that is equidistant from points (0,1) and (5,6) is (2, 4).
that is equidistant from points (0,1) and (5,6) is (2, 4).