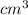Question

Find the volume of the composite solid shown. Round to the nearest tenth.

Answer 1

113.1
`cm^(3)`

Explanation:

The equation to find the volume of a cylinder is:

`V = \pi r^(2) h`

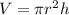
V = volume

r = radius

h = height

The radius of the cylinder is 3 in, and the height of the cylinder is 2 in. Plug these into the equation:

`V = \pi (3)^(2) (2)`

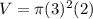
Solve (use calculator):

V =
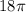`18\pi` or 56.55
`cm^(3)`

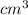
To find the volume of the half sphere use this equation:

`V = (1)/(2)((4)/(3) \pi r^(3) )`

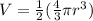
The radius of the circle is 3 in, plug this into the equation:

`V=(1)/(2) ((4)/(3) \pi (3^(3)))`

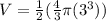
Solve (use calculator):

V =
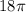`18\pi` or 56.55
`cm^(3)`

To find the volume of the entire shape just add the separate volumes together:

V( of cylinder) + V( of sphere) = Total volume

`56.55 cm^(3)+56.55 cm^(3)= 113.1 cm^(3)`

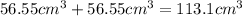
Or, you could rewrite this as 36
`\pi`

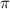
So, the answer is that the volume of the composite solid is 113.1
`cm^(3)`