Question

How do you do this question?

Answer 1

0

Explanation:

∫ sin²(x) cos(x) dx

If u = sin(x), then du = cos(x) dx.

∫ u² du

⅓ u³ + C

⅓ sin³(x) + C

Evaluate between x=0 and x=π.

⅓ sin³(π) − ⅓ sin³(0)

0

Answer 2

`\int\limits^\pi_0 {\sin^2(x)\cos(x)} \, dx=0`

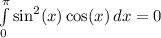
Explanation:

So we have the integral:

`\int\limits^\pi_0 {\sin^2(x)\cos(x)} \, dx`

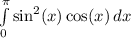
To evaluate this integral, we can use u-substitution. Remember that the derivative of sin(x) is cos(x). So, let u equal sin(x):

`u=\sin(x)`

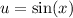
Take the derivative of u:

`(du)/(dx)=\cos(x)`

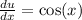
Multiply both sides by dx:

`du=\cos(x)dx`

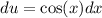
So, we can substitute cos(x) x for du.

We can also substitute sin(x) for u. Thus:

So, our integral is now:

`\int\limits^\pi_0 {\sin^2(x)(\cos(x)} \, dx)\\`

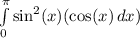
This is equal to:

`=\int\limits^\pi_0 {u^2} \, du`

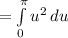
However, we also must change our bounds of integration. To do so, substitute in the lower and upper bound into u. So:

`u=\sin(x)\\u=\sin(0)=0`

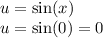
And:

`u=\sin(x)\\u=\sin(\pi)=0`

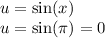
Therefore, our integral with our new bounds is:

`=\int\limits^0_0 {u^2} \, du`

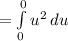
Now, note that the integral has the same upper bound and lower bound. Therefore, this means that our integral is going to be 0 since with the same bounds, there will be no area.

Therefore, our answer is 0:

`\int\limits^0_0 {u^2} \, du=0`

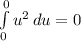
And we're done!