Question

Determine whether the given function is a solution to the given differential equation.

x =2cost - 3sint, x'' +x =0

Answer 1

Given :

A function , x = 2cos t -3sin t .....equation 1.

A differential equation , x'' + x = 0 .....equation 2.

To Find :

Whether the given function is a solution to the given differential equation.

Solution :

First derivative of x :

`x'=(d(2cos t - 3sin t))/(dt)\\\\x'=(d(2cost))/(dt)-((3sint))/(dt)\\\\x'=-2sint-3cost`

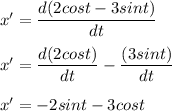
Now , second derivative :

`x''=(d(-2sint-3cost))/(dt)\\\\x''=-(d(2sint))/(dt)-(d(3cost))/(dt)\\\\x''=-2cost+3sint`

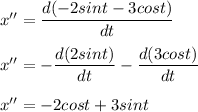
( Note : derivative of sin t is cos t and cos t is -sin t )

Putting value of x'' and x in equation 2 , we get :

=(-2cos t + 3sin t ) + ( 2cos t -3sin t )

= 0

So , x'' and x satisfy equation 2.

Therefore , x function is a solution of given differential equation .

Hence , this is the required solution .