Answer:
1.

2.

3.
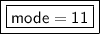
4.
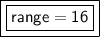
Explanation:
1. Given data : 2 , 3 , 5 , 7 , 8 , 10 , 11 , 11 , 13 , 15 , 17 , 18
Σx = 2 + 3 + 5 + 7 + 8 + 10 + 11 + 11 + 13 + 15 + 17 + 18 = 120
N ( total number of items ) = 12
Finding the mean
To find the mean, divide the sum of all the items by the number of items.
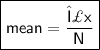


Mean = 10
----------------------------------------------------------
2. Given data : 2 , 3 , 5 , 7 , 8 , 10 , 11 , 11 , 13 , 15 , 17 , 18
N ( total number of items ) = 12
Finding the position of median
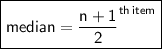
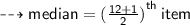
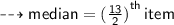
 item
item
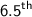 item is the average of 6 th and 7 th items.
item is the average of 6 th and 7 th items.
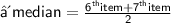

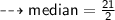

Median = 10.5
-----------------------------------------------------------
3. The mode of a set of data is the value with the highest frequency.
Given data : 2, 3, 5, 7, 8, 10, 11, 11, 13, 15, 17, 18
Here, 11 has the highest frequency.
So, Mode = 11
----------------------------------------------------------
4. Highest number = 18
Lowest number = 2

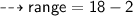
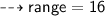
Hope I helped!
Best regards! :D