Question

Find the perimeter of the triangle to the nearest whole unit.

18.
16.
14.
12.

Answer 1

14

Explanation:

Perimeter of the ∆ = sum of the length of the 3 sides.

The length of the 3 sides can be calculated by using the distance formula,
`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`, to find the distance between the vertices of the ∆.

The coordinates of the 3 vertices are:

(-1, 3), (2, 2), (-2, -2)

Distance between (-1, 3) and (2, 2):

Let,

`(-1, 3) = (x_1, y_1)`

`(2, 2) = (x_2, y_2)`

`d = √((2 -(-1))^2 + (2 - 3)^2)`

`d = √((3)^2 + (-1)^2)`

`d = √(9 + 1) = √(10) = 3.2 units`

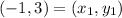
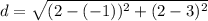
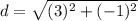
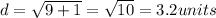
Distance between (2, 2) and (-2, -2)

Let,

`(2, 2) = (x_1, y_1)`

`(-2, -2) = (x_2, y_2)`

`d = √((-2 - 2)^2 + (-2 - 2)^2)`

`d = √((-4)^2 + (-4)^2)`

`d = √(16 + 16) = √(32) = 5.7 units`

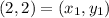
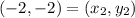
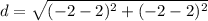
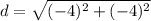
Distance between (-2, -2) and (-1, 3)

Let,

`(-2, -2) = (x_1, y_1)`

`(-1, 3) = (x_2, y_2)`

`d = √((-1 -(-2))^2 + (3 -(-2))^2)`

`d = √((1)^2 + (5)^2)`

`d = √(1 + 25) = √(26) = 5.1 units`

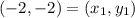
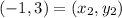
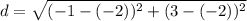
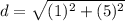
Perimeter of triangle = 3.2 + 5.7 + 5.1 = 14.0 units