Question

12. Higher order Thinking is the Product of two irrational numbers always an irrational number ? Explain​

Answer 1

Not always but sometimes

Explanation:

The product of two irrational numbers is sometimes and not always an irrational number.

So, Let us take two Example:

Example # 1:

Let the two irrational numbers be
`\sf √(37) \ and \ √(2)`

So, Multiplying these will give us

=>
`\sf √(37) * √(2)`

=>
`\sf √(74)`

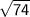
Which is an irrational number.

Example # 2:

Let the two irrational numbers be
`\sf √(2) \ and \ √(2)`

So, Multiplying them would give us:

=>
`\sf √(2) * √(2)`

=>
`\sf (√(2) )^2`

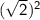
=> 2

Which is a rational number.

This means that the product of two irrational numbers is not always an irrational number but sometimes an irrational number.