Explanation:

Prove the LHS
Using trigonometric identities
That's

Rewrite the expression
We have
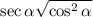
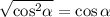
So we have
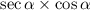
Using trigonometric identities

Rewrite the expression
That's
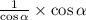
Reduce the expression with cos a
We have the final answer as
1
As proven
Hope this helps you