Sukie interviewed 125 employees at her company and discovered that 21 of them planned to take an extended vacation next year. What is the standard error?

Question

asked Oct 7, 2021 205k views

2 Answers

Konrad Viltersten · Answer 1 · 2021-10-13T23:46:48+0000

Answer:

The standard error is 0.033.

Explanation:

We are given that Sukie interviewed 125 employees at her company and discovered that 21 of them planned to take an extended vacation next year.

Let
$\hat p$ = proportion of employees who planned to take an extended vacation next year

$\hat p$ =
(X)/(n) =
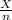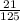(21)/(125) = 0.168

n = number of employees at her company = 125

Now, the standard error is calculated by the following formula;

Standard error, S.E. =
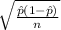
$\sqrt{(\hat p(1-\hat p))/(n) }$

=
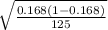
$\sqrt{(0.168(1-0.168))/(125) }$

=
$\sqrt{(0.168 * 0.832)/(125) }$ = 0.033

Hence, the standard error is 0.033.