Question

Pls help !!!!

A video game designer places an anthill at the origin of a coordinate plane. A red ant
leaves the anthill and moves along a straight line to (1, 1), while a black ant leaves the
anthill and moves along a straight line to (1, -1). Next, the red ant moves to (2, 2), while
the black ant moves to (-2,-2). Then the red ant moves to (3, 3), while the black ant
moves to (-3, -3), and so on. Complete the explanation of why the red ant and the black
ant are always the same distance from the anthill,
At any given moment, the red ant's coordinates may be written as (a, a) where a > 0. The
red ant's distance from the anthill is 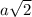. The black ant's coordinates may be written
as (-a, -a) and the black ant's distance from the anthill is 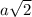. This shows that at
any given moment, both ants are
units from the anthill.

Answer 1

At any given moment, the red ant's coordinates may be written as (a, a) where a > 0. The red ant's distance from the anthill is
`a√(2)` . The black ant's coordinates may be written as (-a, -a) and the black ant's distance from the anthill is
`a√(2)` . This shows that at any given moment, both ants are
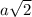`a√(2)` units from the anthill.

Explanation:

Given:

red ant's coordinates written as (a,a)

black ant's coordinates are written as (-a, -a)

To find:

The distance of red and black ants from anthill

Solution:

Compute the distance of red ant from the anthill using distance formula

d (red ant) =
`\sqrt{(a-0)^(2)+ (a-0)^(2)}`

=
`\sqrt{a^(2) + a^(2) }`

=
`\sqrt{2a^(2) }`

=
`a√(2)`

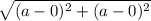
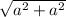
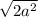
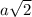
So distance of red ant from anthill is
`a√(2)`

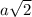
Compute the distance of black ant from the anthill using distance formula

d (black ant) =
`\sqrt{(-a-0)^(2)+ (-a-0)^(2)}`

=
`\sqrt{(-a)^(2) + (-a)^(2) }`

=
`\sqrt{a^(2) + a^(2) }`

=
`\sqrt{2a^(2) }`

=
`a√(2)`

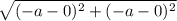
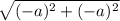
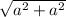
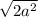
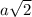
So distance of black ant from anthill is
`a√(2)`

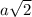
Hence both ants are
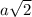`a√(2)` units from the anthill.