Question

Suppose that X and Y are independent random variables from binomial experiments where n = 4 in both cases but the probability of success is p = 0.25 for X and p = 0.5 for Y . Calculate the probability of the events (a) {X = 1, Y = 2}, (b) {X + Y = 1}.

Answer 1

(a) The value of P (X = 1, Y = 2) is 0.1583.

(b) The value of P (X + Y = 1) is 0.1055.

Explanation:

It is provided that:

`X\sim Bin(n=4,p=0.25)\\\\Y\sim Bin(n=4,p=0.50)`

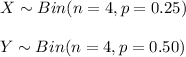
The variables X and Y are independent random variables.

The probability mass function of a Binomial distribution is:

`P(U=u)={n\choose u}(p)^(u)(1-p)^(n-u);\ u=0,1,2,3...`

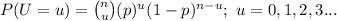
(a)

Compute the value of P (X = 1, Y = 2) as follows:

`P(X=1,Y=2)=[{n\choose x}(p_(x))^(x)(1-p_(x))^(n-x)]* [{n\choose y}(p_(y))^(y)(1-p_(y))^(n-y)]`; Independent

`=[{4\choose 1}(0.25)^(1)(1-0.25)^(4-1)]* [{4\choose 2}(0.50)^(2)(1-0.50)^(4-2)]\\\\=0.422* 0.375\\\\=0.15825\\\\\approx 0.1583`

Thus, the value of P (X = 1, Y = 2) is 0.1583.

(b)

Compute the value of P (X + Y = 1) as follows:

`P(X+Y=1)=P(X=0,Y=1)+P(X=1,Y=0)`

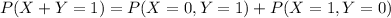
`=\{[{4\choose 0}(0.25)^(0)(1-0.25)^(4-0)]* [{4\choose 1}(0.50)^(1)(1-0.50)^(4-1)]\}\\+\{[{4\choose 1}(0.25)^(1)(1-0.25)^(4-1)]* [{4\choose 0}(0.50)^(0)(1-0.50)^(4-0)]\}\\\\=(0.3164* 0.25)+(0.422*0.0625)\\\\=0.0791+0.0264\\\\=0.1055`

Thus, the value of P (X + Y = 1) is 0.1055.