Answer:
a. F=GMm/r^2; a. M =
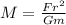
a. F=GMm/r^2; b. r =
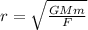
b. M=kxa^3/p^2; a. P =

b. M=kxa^3/p^2; b. a =
![a = \sqrt[3]{(Mp^(2))/(kx) }](https://img.qammunity.org/2021/formulas/mathematics/college/gxqb0x5wv9wwmitppymd831bom68ozrq23.png)
Explanation:
For a. F=GMm/r^2; a. M =
To solve for M, we will rearrange the given equation F=GMm/r^2 such that M is the subject of the formula
From
F=GMm/r^2
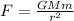
First, Cross multiplication, we then get

Now, divide both sides by
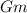
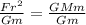
The equation becomes

∴
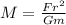
For a. F=GMm/r^2; b. r =
Also, to solve for r, we will rearrange the given equation F=GMm/r^2 such that r is the subject of the formula
From
F=GMm/r^2
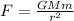
First, Cross multiplication, we then get

Now, divide both sides by
 , Such that we have
, Such that we have
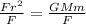
Then,
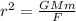
∴
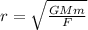
For b. M=kxa^3/p^2; a. P =
To solve for P, we will rearrange the given equation M=kxa^3/p^2 such that P becomes the subject of the formula
From
M=kxa^3/p^2
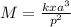
First, Cross multiply, we then get
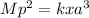
Divide both sides by
 , such that the equation becomes
, such that the equation becomes
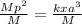
Then,
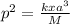
∴

For b. M=kxa^3/p^2; b. a =
To solve for a, we will rearrange the given equation M=kxa^3/p^2 such that a becomes the subject of the formula
From
M=kxa^3/p^2
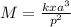
First, Cross multiply, we then get
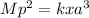
Now, Divide both sides by
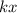 , such that the equation gives
, such that the equation gives
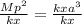
Then,
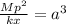
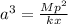
∴
![a = \sqrt[3]{(Mp^(2))/(kx) }](https://img.qammunity.org/2021/formulas/mathematics/college/gxqb0x5wv9wwmitppymd831bom68ozrq23.png)