Question

Just making sure my answers are right. Please show the steps clearly. Thank you so much

Answer 1

Answer: See below

Explanation:

A.

Let's split the integral into two parts, by the Sum Rule.

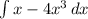`\int\limits {x-4x^3} \, dx` [split into 2 integrals]

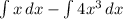`\int\limits {x} \, dx -\int\limits {4x^3} \, dx` [solve integral for each part]

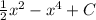`(1)/(2) x^2-x^4+C` [Remember, we need to add C for constant]

-------------------------------------------------------------------------------------------------

B.

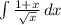`\int\limits {(1+x)/(√(x) ) } \, dx` [expand into 2 integrals]

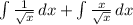`\int\limits {(1)/(√(x) ) } \, dx +\int\limits {(x)/(√(x) ) } \, dx` [simplify second integral]

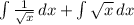`\int\limits {(1)/(√(x) ) } \, dx +\int\limits {√(x) } \, dx` [solve integral for each part]

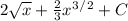
`2√(x) +(2)/(3)x^3^/^2+C`

-------------------------------------------------------------------------------------------------

C.

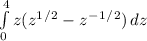`\int\limits^4_0 {z(z^1^/^2-z^-^1^/^2)} \, dz` [distribute]

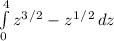`\int\limits^4_0 {z^3^/^2-z^1^/^2} \, dz` [split into 2 integrals]

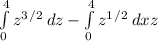`\int\limits^4_0 {z^3^/^2} \, dz -\int\limits^4_0 {z^1^/^2} \, dxz` [solve integral for each part]

`(64)/(5) -(16)/(3)` [solve]

`(112)/(15)`

-------------------------------------------------------------------------------------------------

D. *Note: I can't put -1 for the interval, but know that the 1 on the bottom is supposed to be -1.

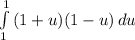`\int\limits^1_1 {(1+u)(1-u)} \, du` [expand]

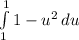`\int\limits^1_1 {1-u^2} \, du` [split into 2 integrals]

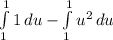`\int\limits^1_1 {1} \, du-\int\limits^1_1 {u^2} \, du` [solve integral for each part]

`2-(2)/(3)` [solve]

`(4)/(3)`