Question

Use the Ratio Test to determine the convergence or divergence of the series. If the Ratio Test is inconclusive, determine the convergence or divergence of the series using other methods. (If you need to use or –, enter INFINITY or –INFINITY, respectively.)

[infinity]summation 7 n!/n = 1

Answer 1

Given series is divergent

Explanation:

Step(i):-

By using Ratio test

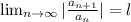
`\lim_(n \to \infty) |(a_(n+1) )/(a_(n) ) | = l`

a)
`\lim_(n \to \infty) |(a_(n+1) )/(a_(n) ) | = l`

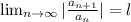
'l' is finite then the given ∑aₙ is convergent

b)
`\lim_(n \to \infty) |(a_(n+1) )/(a_(n) ) | = l`

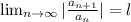
Here 'l' is infinite then the ∑aₙ is divergent

Step(ii):-

Given aₙ =
`(n!)/(n)`

`a_(n+1) = ((n+1)!)/(n+1)`

`\lim_(n \to \infty) |(a_(n+1) )/(a_(n) ) | = \lim_(n \to \infty) |(((n+1)!)/(n+1) )/((n!)/(n) ) |`

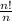
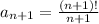
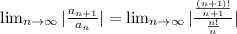
we know that n ! = n (n-1) (n-2) ......3.2.1

and also (n+1) ! = (n+1)n!

`\lim_(n \to \infty) |(a_(n+1) )/(a_(n) ) | = \lim_(n \to \infty) |((n+1)n!)/(n+1) )/((n!)/(n) ) |`

`\lim_(n \to \infty) |(a_(n+1) )/(a_(n) ) | = \lim_(n \to \infty) n`

= ∞

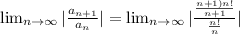
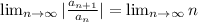
Given sum of the series is divergent